前言

今天要介紹的是「降維」的機器學習方法 PCA 以及一些 PCA 的延伸應用( PCR 、 PLS )。

主成分分析 PCA

• 主成分分析 PCA

• 主成分迴歸 PCR

• 偏最小平方迴歸 PLS

主成分分析 PCA

主成分分析(Principal components analysis, PCA)是一種非監督式(Un-supervised)的機器學習方法，可以用來分群(Clustering)，通常使用的資料一開始是沒特別標記、分類的(Un-labeled Y)。

使用主成分分析 PCA的時機同嘗試用在降低資料維度，避免變數的共線性問題，當維度很大時可以減少運算量並避免模型 overfitting(使用太多不必要的變數)。

主成份分析的目標是以較少的變數(主成份們)來解釋最多的變異。第一主成分C1可以解釋最多的變異，第二主成分C2則和C1獨立(正交、相關係數為0)避免與C1訊息重疊，並盡可能使資料在該軸的變異數最大。以此類推，解釋量依次遞減。

從下圖可以看到第一主成分(綠色)上可以投影出最分散的資料，代表它能解釋最多的變異。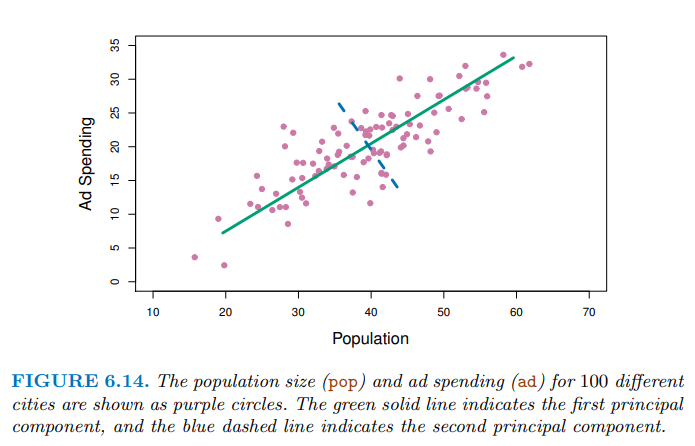

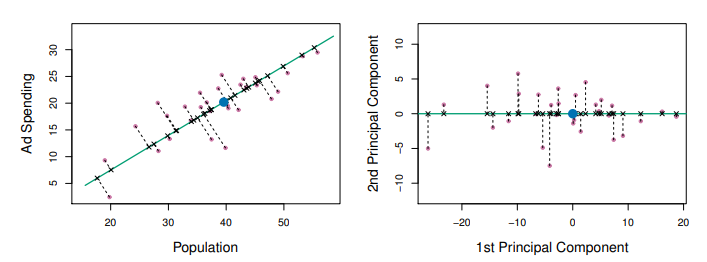
主成分是由各變數的標準化線性組合(normalized linear combination)而成，會去限制這些負荷向量loadings vectors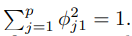的平方總和為一。接著再由目標:「解釋最多的變異」去做最佳化並求解(利用 eigen decomposition 求解)得出這些負荷向量的值。

第一主成分組合式子: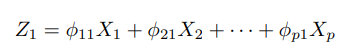

最佳化求解: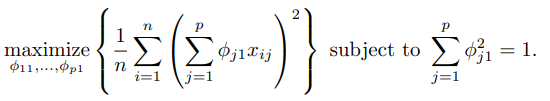

[R code] PCA

Genomic data 常常會去應用到PCA和分群的方法，這邊以ISLR2套件中的 NCI60 cancer cell line microarray data 做 PCA 範例:

## 載入、觀察資料
install.packages("ISLR2")
library (ISLR2)
nci.labs <- NCI60$labs # (Y, label) cancer types
nci.data <- NCI60$data
dim (nci.data) # 64 rows and 6,830 columns
table (nci.labs) # cancer types

使用prcomp()函式可以進行主成分分析:

## 主成分分析PCA, perform PCA on the data after scaling the variables (genes) 
pr.out <- prcomp (nci.data , scale = TRUE)

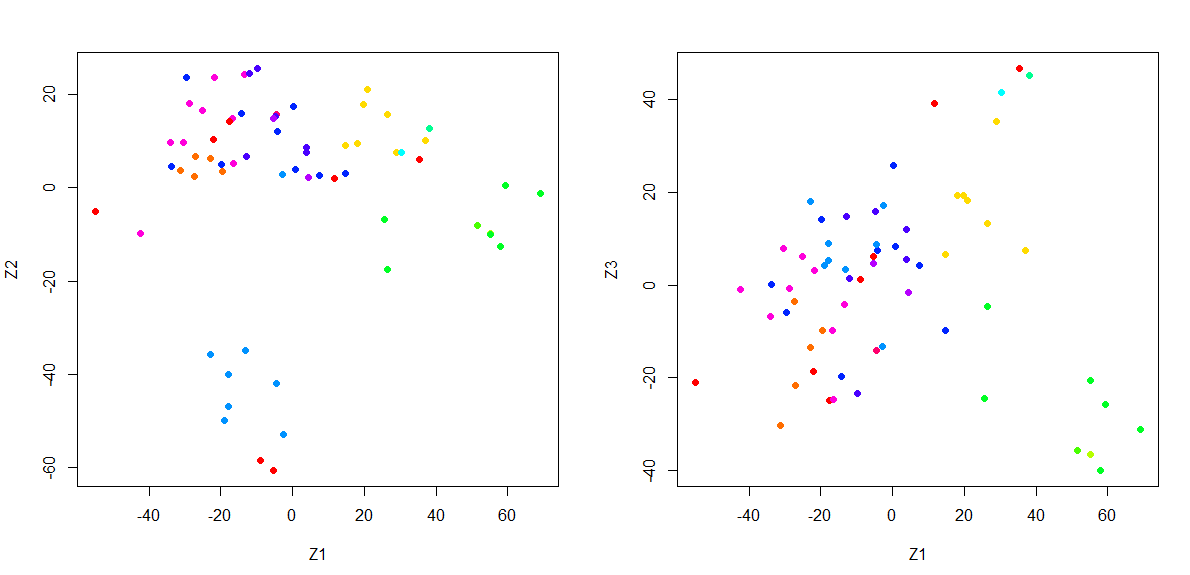
畫出資料在 主成分Z1、Z2, 主成分 Z1、Z3 的分布情形:
在不知道確切資料們是什麼類別(Y, label)的時候，透過觀察前幾個主成分，我們可以觀察到有相似特性的資料會聚集再一起，因此可以被進一步應用再「分群」上。
以這個資料為例，將癌症種類(cancer types)套色，我們可以清楚看到同一類的癌症資料在 [主成分Z1、Z2], [主成分 Z1、Z3]的二為分布上都分布在相近的地方:

par (mfrow = c(1, 2))
# Assign a color to each of the 64 cell lines, based on the cancer type to which it corresponds.
Cols <- function (vec) {  
  cols <- rainbow ( length ( unique (vec)))
  return (cols[as.numeric (as.factor (vec))])
  }
plot (pr.out$x[, 1:2], col = Cols (nci.labs), pch = 19,
        xlab = "Z1", ylab = "Z2")
plot (pr.out$x[, c(1, 3)], col = Cols (nci.labs), pch = 19,
        xlab = "Z1", ylab = "Z3")

解釋變異 Proportion of Variance Explained (PVE):

summary (pr.out)

> summary (pr.out)
Importance of components:
                           PC1      PC2      PC3      PC4      PC5      PC6
Standard deviation     27.8535 21.48136 19.82046 17.03256 15.97181 15.72108
Proportion of Variance  0.1136  0.06756  0.05752  0.04248  0.03735  0.03619
Cumulative Proportion   0.1136  0.18115  0.23867  0.28115  0.31850  0.35468
...

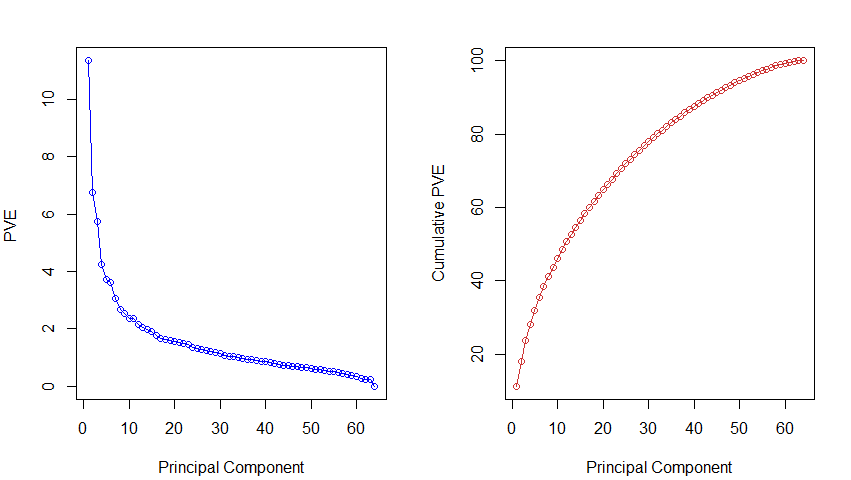
解釋比例比例(%):

##解釋比例比例(%)
# 從pca中取出標準差(pca$sdev)後再平方，計算variance(特徵值)
# 解釋比例 = 各個主成份的特徵值/總特徵值
pve <- 100 * pr.out$sdev^2 / sum (pr.out$sdev^2) 

plot (pve , type = "o", ylab = "PVE ",
      xlab = " Principal Component ", col = " blue ")
#累積解釋比例圖, 累積每個主成份的解釋比例(aggregated effects)
plot ( cumsum (pve),  # 累加前M個主成份元素的解釋比例值
       type = "o",  col = " brown3 ",
       ylab = " Cumulative PVE ",xlab = " Principal Component ")

[補充] PCR

PCR(Principal Component Regression)主成分迴歸，是使用 PCs 去建立迴歸模型進行分析，它仍然是一種非監督式的方法，因為在決定主成分時並沒有使用到 Y 的資訊。因此 PCR 不能保證
( PCs )最能解釋預測變量(X)的方向也將是最好用來預測(Y)的方向。

PCR可以解決變數共線性( multicollinearity )的問題，藉由篩選去除少貢獻度的 PCs ，可以達到降維的效果，也可以提升預測的準確率。

[注意] 雖然PCR提供了降維的效果(使用較少維度的解釋變數)，但它並沒有變數篩選的效果。

• [R code]

使用pls 套件的 pcr( )進行 PCR 建模。
資料 P 維，(M < p)，想取 M 維的解釋變數:

install.packages("pls")
library (pls)

pcr.fit <- pcr ( Y ∼ ., data = data , 
                scale = TRUE , # scale = TRUE代表標準化 X predictor
                validation = "CV") # compute the ten-fold cross-validation error( RMSE root mean squared error) for each possible value of M
summary (pcr.fit) # 提供 % variance explained，解釋變異的累加百分比

## cross-validation MSE
# 用來決定 first M principal components
validationplot (pcr.fit , val.type = " MSEP ") 

補充R CODE

[補充] PLS

PLS( Partial Least Squares )偏最小平方迴歸，是一種監督式的方法，和 PCR 相同是一種降維的方法，但不同在於 PLS 的 Y 也會進行投影、轉軸。

它通過投影預測變數和觀測變數到一個新空間來尋找一個線性迴歸模型，並試圖找到 X 的多維方向來解釋最大的 Y 變異。

• [R code]

使用pls 套件的 plsr( )進行 PCR 建模。

## 切割 train, test
 set.seed (1)
train <- sample (1: nrow (x), nrow (x) / 2)
test <- (-train)
y.test <- y[test]

## PLS model
pls.fit <- plsr (Y ∼ ., data = data , subset = train ,scale = TRUE , validation = "CV")
summary (pls.fit)
validationplot (pls.fit , val.type = " MSEP ")

## predict( )
pls.pred <- predict (pls.fit , x[test , ], ncomp = 1)
mean ((pls.pred - y.test)^2) # MSE

參考資料、網站、書籍

An Introduction to Statistical Learning with Applications in R. 2nd edition. Springer. James, G., Witten, D., Hastie, T., and Tibshirani, R. (2021).

Principal Component Regression(@Ewa Sobolewska)
https://rpubs.com/esobolewska/pcr-step-by-step

主成分分析, 維基百科
https://zh.wikipedia.org/zh-tw/%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90

Principal Components Analysis (PCA) | 主成份分析 | R 統計
https://jamleecute.web.app/principal-components-analysis-pca-%E4%B8%BB%E6%88%90%E4%BB%BD%E5%88%86%E6%9E%90/